How To Find Holes Of A Rational Function
HOW TO FIND THE HOLE OF A RATIONAL FUNCTION
In this section, you will larn how to discover the hole of a rational function
And we will exist able to find the hole of a part, only if it is a rational function.
That is, the function has to be in the course of
f(x) = P/Q
Example : Rational Function
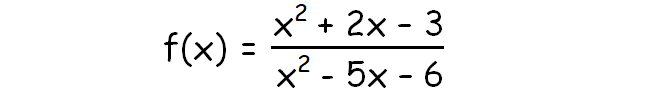
Steps Involved in Finding Pigsty of a Rational Part
Permit y = f(10) be the given rational function.
Footstep 1 :
If information technology is possible, factor the polynomials which are plant at the numerator and denominator.
Step 2 :
After having factored the polynomials at the numerator and denominator, we have to see, whether in that location is any common factor at both numerator and denominator.
Instance 1 :
If there is no common factor at both numerator and denominator, there is no pigsty for the rational role.
Example ii :
If in that location is a common gene at both numerator and denominator, there is a hole for the rational role.
Step 3 :
Let (x - a) be the common factor found at both numerator and denominator.
Now we have to make (x - a) equal to zero.
When we do so, nosotros go
10 - a = 0
x = a
And so, at that place is a hole atx = a.
Step 4 :
Allow y = b for x = a.
So, the pigsty will appear on the graph at the point (a, b).
Examples
Example 1 :
Detect the pigsty (if whatever) of the function given below
f(x) = 1 / (x + 6)
Solution :
Step i:
In the given rational function, clearly there is no common gene found at both numerator and denominator.
Step 2 :
So, there is no hole for the given rational function.
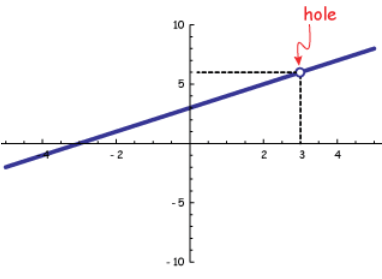
Example 2 :
Notice the hole (if whatever) of the office given beneath.
f(10) = (x2+ 2x - 3) / (x2- 5x + vi)
Solution :
Stride ane:
In the given rational function, let u.s. cistron the numerator and denominator.
f(ten) = [(10 + 3)(ten - 1)] / [(ten - 2)(x - 3)]
Step 2 :
Afterward having factored, there is no common factor establish at both numerator and denominator.
Pace iii :
Hence, in that location is no hole for the given rational function.
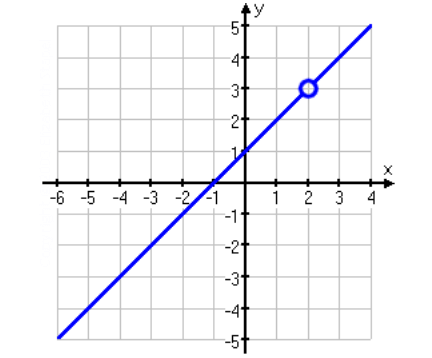
Example 3 :
Detect the hole (if whatever) of the role given below.
f(x) = (tenii - ten - two) / (x - ii)
Solution :
Footstep one:
In the given rational function, let us factor the numerator .
f(x) = [(x-2)(x+1)] / (x-2)
Stride 2 :
Afterwards having factored, the common gene found at both numerator and denominator is (x - 2).
Step three :
At present, we have to brand this common factor (ten-2) equal to zero.
x - 2 = 0
ten = ii
So, there is a hole at
x = two
Step four :
After crossing out the mutual factors at both numerator and denominator in the given rational role, nosotros get
f(x) = x + 1 ------(one)
If we substitute two for 10, we get become
f(2) = 3
Then, the hole volition announced on the graph at the betoken (2, 3) .

Apart from the stuff given in this section, if yous need whatever other stuff in math, please employ our google custom search here.
Kindly mail service your feedback tov4formath@gmail.com
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
Source: https://www.onlinemath4all.com/how-to-find-the-hole-of-a-rational-function.html
Posted by: sowellholed1992.blogspot.com


0 Response to "How To Find Holes Of A Rational Function"
Post a Comment